* 主体类型
* 企业名称
* 信用代码
* 所在行业
* 企业规模
* 所在职位
* 姓名
* 所在行业
* 学历
* 工作性质
请先选择行业
您还可以选择以下福利：
行业福利，领完即止！
下载app免费领取会员
三维曲线是指在三维空间中的曲线。它是由变量 x，y 和 z 的方程所确定的曲线。三维曲线在许多领域中都有应用，包括物理学、数学、计算机图形学等。
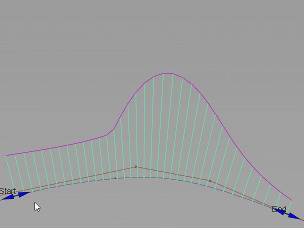
三维曲线的指代范围是指曲线所能描述的对象或现象的范围。具体来说，三维曲线可以用来描述各种各样的对象，包括自然界中的物体、建筑结构、运动轨迹等。
首先，三维曲线可以用来描述自然界中的物体。例如，我们可以使用三维曲线来描述山脉的形状、水流的路径、树木的分支等。通过对这些物体进行建模和分析，我们可以更好地理解它们的特征和行为。
其次，三维曲线可以用来描述建筑结构。在建筑设计过程中，三维曲线可以被用来描述建筑物的形状和结构。通过使用三维曲线，建筑师可以更好地预测建筑物的外观和性能，并做出相应的优化和改进。
另外，三维曲线还可以用来描述运动轨迹。在物理学和运动学中，三维曲线被用来描述物体在三维空间中的运动。例如，通过对一个运动物体的轨迹进行建模和分析，我们可以推断出它的速度、加速度和路径等信息。
除了以上应用，三维曲线还广泛应用于计算机图形学领域。在计算机生成图像的过程中，三维曲线被用来描述虚拟物体的形状和运动。通过对这些曲线的渲染和处理，我们可以生成逼真的三维图像和动画。
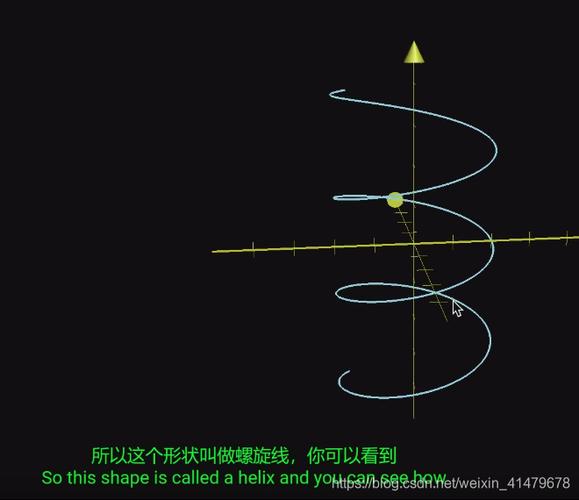
总之，三维曲线的指代范围非常广泛，涵盖了自然界中的物体、建筑结构、运动轨迹以及计算机图形学等领域。通过对这些曲线的分析和建模，我们可以更好地理解和探索我们周围的世界。
本文版权归腿腿教学网及原创作者所有，未经授权，谢绝转载。
- Dynamo教程 | Dynamo是什么软件？Dynamo如何让Revit在建筑信息管理方面更进一步？
- Dynamo教程 | 最新节点
- Dynamo教程 | 无法访问Dynamix
- Dynamo教程 | 设计步骤的参数化化
- Dynamo教程 | 如何学习Dynamo？Dynamo该如何入门？
- Dynamo教程 | Vibrant Visuals: Unleashing the Power of Dynamic Graphics
- Dynamo教程 | 什么是3维曲线数学公式T的含义
- Dynamo教程 | dynamo自定义节点指南
- Dynamo教程 | 参数化DDT全程
- Dynamo教程 | 什么是Dynamo？如何运用Dynamo自动化创建Revit机电样板？
