下载app免费领取会员
绘制三维曲线是计算机图形学中的一个重要任务，它可以帮助我们可视化复杂的曲线形状。在本文中，我们将介绍几种常用的方法来绘制三维曲线。
1. 参数方程法
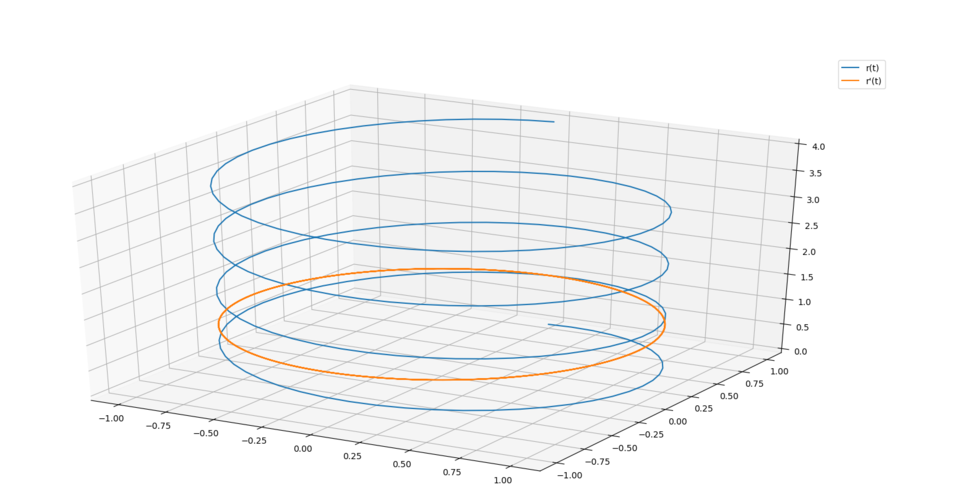
参数方程法是最常用的绘制三维曲线的方法之一。它将三维曲线的坐标表示为参数的函数。例如，给定参数t，我们可以使用以下参数方程来表示一条三维曲线：
x = f(t), y = g(t), z = h(t)
在参数方程法中，我们可以选择不同的函数f(t)，g(t)和h(t)来得到不同的曲线形状。常见的参数方程包括圆柱曲线、抛物线、螺旋曲线等。
2. 点集插值法
点集插值法是一种通过给定的点集来逼近三维曲线的方法。该方法通常用于曲线绘制和曲面建模。在点集插值法中，我们需要先给定一组控制点，然后通过插值算法来计算中间的点。
常见的点集插值方法包括贝塞尔曲线和B样条曲线。贝塞尔曲线通过控制点来定义曲线形状，而B样条曲线通过在控制点之间插入额外的点来逼近曲线形状。
3. 参数化曲线法
参数化曲线法是一种通过在曲线上移动一个参数来绘制曲线的方法。在参数化曲线法中，我们首先需要选择一个基本的曲线形状（如直线或圆），然后通过变换参数来改变曲线形状。
参数化曲线法可以用于绘制复杂的曲线形状，如螺旋线、椭圆和心形曲线。它也常用于动画和特效的制作中。
4. 数学函数法
数学函数法是一种直接使用数学函数来定义三维曲线形状的方法。在数学函数法中，我们可以通过定义直角坐标系或极坐标系下的数学函数，来表示曲线上的点的坐标。
数学函数法可以用于绘制各种曲线形状，包括线性函数、幂函数、三角函数和指数函数等。
5. 曲面延拓法
曲面延拓法是一种通过将二维曲线延拓到三维空间中来绘制三维曲线的方法。在曲面延拓法中，我们首先需要选择一条二维曲线，然后通过在曲线的每个点上加入新的维度来将其延拓到三维空间中。
曲面延拓法可以用于绘制各种复杂的曲线形状，如环形曲线、螺旋曲线和超椭圆曲线等。
绘制三维曲线是计算机图形学中的一个重要任务，它可以帮助我们可视化复杂的曲线形状。在本文中，我们介绍了几种常用的方法来绘制三维曲线，包括参数方程法、点集插值法、参数化曲线法、数学函数法和曲面延拓法。每种方法都有其适用的场景和特点，选择合适的方法可以帮助我们更好地绘制出所需的曲线形状。
本文版权归腿腿教学网及原创作者所有，未经授权，谢绝转载。
- Dynamo教程 | dynaform5.9.4安装指南
- Dynamo教程 | 什么是参数化设计？
- Dynamo教程 | Dynamically Powered: The Gold Standard
- Dynamo教程 | 使用List.stream.filter来筛选多个数据
- Dynamo教程 | DOM节点的含义是什么？
- Dynamo教程 | Dyna产生的约束反力
- Dynamo教程 | 为什么Dynamo无法呈现图像？
- Dynamo教程 | dynamo建模的优点: 解析dynamo建模的好处
- Dynamo教程 | 自定义节点在Dynamo中的应用
- Dynamo教程 | 安装dynamo自定义节点包
