下载app免费领取会员
在计算机图形学中，Dynamo是一种常见的旋转实现方法。它通过应用数学变换来实现对象的旋转，使得对象在三维空间中以任意轴进行旋转。
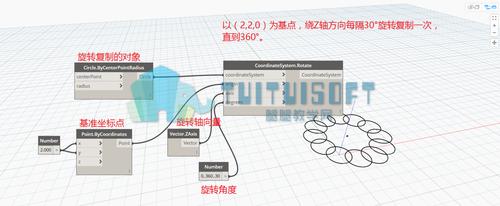
旋转是图形学中的一项基本操作，它能够改变对象的位置和方向。在Dynamo方法中，旋转是通过应用一个旋转变换矩阵来实现的。这个矩阵定义了一个用于旋转的轴，以及旋转的角度。
为了实现Dynamo的旋转方法，首先需要确定旋转轴的位置和方向。旋转轴可以是任意的向量，它可以通过定义两个点来确定。旋转轴的方向是与这两个点的向量方向相同的单位向量。
一旦旋转轴被确定，接下来就可以计算旋转变换矩阵了。旋转变换矩阵是一个三维变换矩阵，它可以将对象旋转指定的角度。在计算旋转变换矩阵时，需要使用旋转角度和旋转轴。
计算旋转变换矩阵的方法比较简单。首先需要将旋转角度转换为弧度制，然后使用三角函数计算旋转矩阵的各个元素。旋转变换矩阵的计算公式如下：
其中θ是旋转角度，ux，uy，uz是旋转轴的坐标。
一旦旋转变换矩阵被计算出来，就可以将其应用到对象上。应用旋转变换矩阵时，需要将对象的每个顶点坐标与矩阵相乘。相乘的结果就是旋转后的对象坐标。
除了旋转变换矩阵，还可以使用四元数来实现Dynamo的旋转方法。四元数是一种用于表示旋转的数学工具，它可以更高效地进行旋转计算。使用四元数进行旋转时，可以将旋转角度和旋转轴转换为四元数表示，然后将四元数与对象进行插值运算。
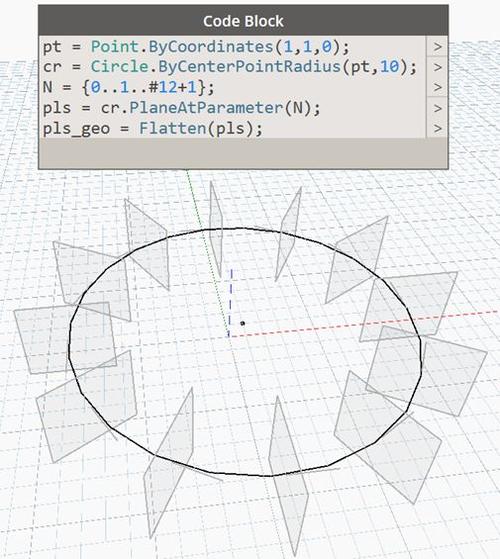
总结起来，Dynamo的旋转实现方法使用旋转变换矩阵或四元数来实现对象的旋转。旋转变换矩阵通过计算旋转轴和旋转角度来确定，然后将其应用到对象上。而四元数则更高效地进行旋转计算，通过插值运算来实现对象的平滑旋转。
本文版权归腿腿教学网及原创作者所有，未经授权，谢绝转载。
